Sobat Aku-Pembelajar sekarang kita membahas mengenai kuat medan listrik, namun sebelumnya kita pahami dulu mengenai :
Pengertian Medan Listrik
Gaya yang timbul di antara dua buah partikel bermuatan yang dipisahkan pada suatu jarak tertentu tanpa kontak antara keduanya disebut action at adistance.
Medan adalah ruang di sekitar benda yang setiap titik dalam ruang tersebut akan terpengaruh oleh gaya yang ditimbulkan benda. Jika partikel menghasilkan gaya listrik, maka medan yang timbul di sekitar partikel itu disebut medan listrik.
Dengan demikian dapat dikatakan bahwa medan listrik adalah daerah di sekitar muatan listrik yang masing – masing dipengaruhi oleh gaya listrik.
Medan listrik merupakan besaran vektor yang arahnya didefinisikan sebagai arah gaya yang dialami oleh suatu benda bermuatan positif.
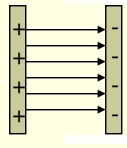
Medan listrik direpresentasikan dengan garis- garis khayal yang menjauhi (atau keluar) muatan positif dan mendekati (atau masuk) muatan negatif. Kerapatan garis- garis gaya lsitrik menunjukkan besarnya kuat medan listrik.
Gaya Coulomb
Di sekitar muatan sumber q terdapat medan listrik sehingga muatan q yang diletakkan dalam pengaruh medan listrik ini mendapat gaya Coulomb. Muatan lain q2 yang diletakkan dalam pengaruh medan listrik ini juga mendapat gaya Coulomb.
Gaya Coulomb yang dialami oleh partikel bermuatan bergantung pada muatan partikel dan muatan sumber q. Untuk mengetahui efek medan listrik dari muatan sumber q, maka diletakkan suatu muatan uji dalam ruang di seitar medan listrik tersebut.
Garis Gaya
Di sekitar muatan listrik, baik muatan positif maupun negatif timbul garis gaya. Kuat medan listrik pada suatu titik menyinggung garis gaya. Di tempat yang bermedan kuat garis gaya dilukiskan rapat. Bila medan lemah garis gaya dilukiskan renggang.
- Arah medan menyinggung garis gaya listrik
- Arah garis gaya keluar dari muatan positif
- Arah garis gaya masuk ke mauatan negatif
- Kuat medan dinyatakan oleh rapat garis gaya
Cara Menghitung Kuat Medan Listrik.
Kuat medan listri E didefinisikan sebagai hasil bagi gaya Coulomb yang bekerja pada muatan uji dengan besar muatan uji tersebut yaitu q0. Jadi kuat medan listrik menyatakan besarnya muatan listrik. Secara matematis kuat medan listrik dapat ditulis sebagai berikut
E = F/q0
E = kuat medan listrik, N/C
F = gaya yang dialami muatan uji, N
q0 = besar muatan uji, C
Gambar a. Muatan uji positif disimpan pada jarak r dari muatan sumber positif. Muatan uji mendapat gaya tolak dari muatan sumber. Arah gaya pada muatan uji menjauhi muatan sumber. Dan Arah medan listriknya menjauhi muatan sumber.
Gambar b. Muatan sumber negative. Arah gaya pada muatan uji menuju muatan sumber, terjadi Tarik menarik, sehingga arah medan listriknya menuju muatan negative. Dengan demikian dapat dikatakan bahwa arah medan listrik di sekitar muatan sumber positif selalu menjauhi muatan sumbernya dan sebaliknya, arah medan listrik di sekitar muatan sumber negative selalu menuju ke muatan tersebut.
1). Contoh Soal Dan Pembahasan Ujian Materi Kuat Medan Listrik
Titik P berjarak 30 cm dari sebuah muatan yang besarnya q = 25mC.
Hitung besar dan tentukan arah medan listrik di titik P
Jawab dan Pembahasan.
Diketahui:
r = 0,3m
q = 25mC = 2,5 x 10-5 C
kuat medan listrik di titik P adalah:
E = k q/(r2)
E = (9 x 109Nm2/C2) x( 2,5 x 10-5C) / (0,3m)2 = 2,5 x 106 N/C
Dan Arah medan listriknya menjauh muatan q.
2). Contoh Soal Dan Pembahasan Ujian Materi Kuat Medan Listrik
Hitung kuat medan listrik pada jarak 1 cm dari sebuah muatan positif 10-6 coulomb dan tentukan arah medan listriknya…
Jawaban dan Pembahasan:
Diketahui:
Muatan sumber q = 10-6 C
Jarak titik A ke muatan sumber r = 1 cm = 10-2 m
Tetapan k = 9×109 Nm2C-2
Besar kuat medan listrik dapat dihitung dengan persamaan berikut:
E = k q/(r2)
E = (9 x109) (10-6)/ (10-2)2
E = 9 x 107 N/C
Arah kuat medan listrik E adalah menjauhi muatan sumber q.
3). Contoh Soal Perhitungan Arah Kuat Medan Titik P
Sebuah titik P berada pada jarak 20 cm dari sebuah muatan q = 16 μC. Hitung besar dan arah medan lisrik di titik P.
Dan hitung percapatan awal jika sebuah muatan q = 5μC yang bermassa 3 gram dilepaskan dari titik P.
Diketahui:
q = 16 μC = 1,6 x 10-5 C
r = 20 cm = 0,2 m
m = 3 gram
Menghitung Kuat Medan Di Titik P
Ep = k q/(r)2
EP = 9×109(1,6×10-5)/(0,2)2
EP = 3,6 x106 N/C
Muatan q adalah positif, jadi Arah Medan Listriknya Menjauhi muatan q
Rumus Menghitung Percepatan Muatan Di Medan Listrik Titik P
Besarnya percepatan sebuah partikel yang berada dalam medan listrik di titik P dapat dihitung dengan Hukum Newton 2 seperti berikut:
F = m.a atau
a = F/m
a = percepatan awal partikel
m = massa partikel
F = Gaya yang diterima partikel dalam medan listrik di titik P.
Menghitung Gaya Elektrostatik Partikel Dalam Medan Listrik Di Titik P
Besar gaya dalam medan listrik di titik P dapat dinyatakan dengan rumus berikut:
F = q EP
q = 5 μC = 5 x10-6 C
Diketahui dari perhitungan di atas
EP = 3,6 x106 N/C
FP = (5 x10-6)(3,6 x106)
FP = 18 N
Maka Percepatan awal partikel adalah
a = F/m
m = 3 gram = 3 x 10-3 kg
a = 18/(3 x10-3)
a = 6 x10-3 m/s2
Jadi, Ketika partikel berada dalam medan listrik di titik P, maka akan bergerak dengan percepatan awal 6 x10-3 m/s2.
4). Contoh Soal Rumus Kuat Medan Listrik Antara Dua Muatan
Sebuah titik partikel P berada tepat ditengah tengah antara dua muatan yang berjarak 10 cm seperti tampak pada gambar. Muatan partikel q1 = 2×10-6 C dan muatan q2 = 5×10-6 C.
a). Hitunglah kuat medan listrik di titik P
b). Hitung gaya listrik yang terjadi pada pertikel yang bermuatan -5 x 10-8 C ketika berada di titik P
Jawab:
Muatan uji P biasanya diasumsikan sebagai muatan positif
E1 = kuat medan listrik akibat q1
E2 = kuat medan listrik akibat q2
Menghitung Kuat Medan Listrik Di Titik P Akibat Muatan Listrik q1
E1 = k (q1)/(r1)2
E1 = (9×109)(2×10-6)/(0,05)2
E1 = 7,2×106 N/C
Menghitung Kuat Medan Listrik Di Titik P Akibat Muatan Listrik q2
E2 = k (q2)/(r2)2
E2 = (9×109)(5×10-6)/(0,05)2
E2 = 18 x106 N/C
Rumus Menghitung Kuat Medan Listrik Di Titik P Antara Dua Muatan Listrik
Kuat Medan Listrik yang dialami oleh titip P yang disebabkan oleh dua muatan q1 dan q2 dapat dinyatakan dengan rumus berikut:
EP = E1 + E2
EP = 7,2×106 + 18×106 N/C
EP = 25,2 x 106 N/C
Jadi kuat medan listrik yang dialami di titik P adalah EP = 25,2 x 106 N/C
Menghitung Gaya Listrik Muatan Di Titik P
Untuk Menghitung gaya listrik partikel pada titik P yang bermuatan -5 x 10-8 C dapat dinyatakan dengan rumus berikut:
FP = EP x q
FP = (25,2 x 106) x (-5 x 10-8)
FP = -1,26 N
Tanda negative menunjukkan arah gaya FP adalah ke kiri.
5). Contoh Soal Perhitungan Jarak Muatan Pada Kuat Medan Listrik Nol
Dua buah muatan A dan B memiliki muatan listrik masing masing +4×10-8 C, dan +16×10-8 C yang terpisah pada jarak 6 cm. Tentukan Posisi titik P agar kuat medan listriknya = 0
Diketahui:
q1 = +4×10-8 C,
q2 =+16×10-8
r = 6 cm
r = r1 + r2
Rumus Menghitung Kuat Medan Listrik Di Titik P Antara Dua Muatan Listrik
Kuat Medan Listrik yang dialami oleh titip P yang disebabkan oleh dua muatan q1 dan q2 dapat dinyatakan dengan rumus berikut:
EP = E1 + E2
Kuat medan dititik P sama dengan nol atau
EP = 0,
karena q1 dan q2 beruatan positif maka arahnya berlawanan, sehingga
E1 + (-E2) = 0 atau
E1 = E2
Jika jarak P dari q1 adalah x, maka jarak P dari q2 adalah 6 – x sehingga
r1 = x
r2 = 6 – x
Menghitung Jarak Pada Kuat Medan Nol
Besar kuat medan di titip P adalah nol akibat E1 dan E2 dapat dinyatakan dengan rumus berikut:
E1 = E2
E1 = k (q1)/(r1)2
E2 = k (q2)/(r2)2
Substitusikan semua bersaran E1 dan E2 ke dalam persamaan rumus, sehingga diperoleh seperti berikut:
k (q1)/(r1)2 = k (q2)/(r2)2
(q1)/(r1)2 = (q2)/(r2)2
(q1)(r2)2 = (q2)(r1)2
Substitusikan nilai q1, q2, r1 dan r2 ke dalam persamaan, sehingga seperti berikut
(4×10-8)(6-x)2 = (16×10-8)(x)2
4 × (6-x)2 = (16)(x)2
(6-x)2 = (4)(x)2
36 -12x+x2 = 4x2
3x2 +12x – 36= 0
(x + 6)(x – 2) = 0
Akhirnya diperoleh
x = – 6 cm
x = 2 cm
Jarak titik P dari q1 adalah r1
r1 = x
r1 = 2 cm
Jarak titik P dari q2 adalah r2
r2 = 6 – x
r2 = 6 – 2
r2 = 4 cm
Jadi letak titik P berada 2 cm di sebelah kanan q1 atau 4 cm di sebelah kiri q2.
6). Contoh Soal Perhitungan Kuat Medan Nol Antara Dua Muatan.
Dua buah muatan masing masing q1 = 9 μC da q2 = 16 μC terpisah satu dengan lainnya pada jarak 14 cm. Titik P terletak sedemikian, sehingga kuat medan pada titik P sama dengan Nol. Tentukan posisi titik P dari muatan q1.
Diketahui:
q1 = 9 μC = 9 x 10-6 C
q2 = 16 μC = 16 x 10-6 C
r = 14 cm
Catatan:
Kuat medan di titik P merupakan resultan kuat medan listrik yang ditimbulkan oleh kedua muatan q1 dan q2.
Resultan kuat medan akan sama dengan nol pada titik P jika kedua kuat medan adalah sama namun berlawanan arah, dan titik P berada pada garis lurus antara q1 dan q2. pernyataan ini dapat dirumuskan seperti berikut
E1 = E2
E1 = k (q1)/(r1)2
E2 = k (q2)/(r2)2
Substitusikan semua beraran E1 dan E2 ke dalam persamaan rumus, sehingga diperoleh seperti berikut:
k (q1)/(r1)2 = k (q2)/(r2)2
(q1)/(r1)2 = (q2)/(r2)2
(q1)/(q2) = (r1)2/(r2)2
Substitusikan nilai q1 dan q2 ke dalam persamaan di atas
(9×10-8)/(16×10-8)= (r1)2/(r2)2
9/16 = (r1)2/(r2)2
(r1)/(r2) = Ö(9/16)
r1/r2 =3/4
r1: r2 = 3:4
Dengan demikian r1 adalah
r1 = 3/(3+4) x 14
r1 = 6 cm
r1 = merupakan jarak titip P dari q1
r2 = 14 – 6
r2 = 8 cm
r2 = merupakan jarak titip P dari q2
https://ardra.biz/kuat-medan-listrik/
https://www.fisika.co.id/2020/10/medan-listrik.html
http://staff.uny.ac.id/sites/